Google Ads
Module 4.2
Series & Parallel Resistors
- After studying this section, you should be able to:
- Calculate total resistance values in series resistance networks.
- Use appropriate formulae to calculate resistance in Parallel resistance networks.
- • Reciprocal of the sum of reciprocals.
- • Product over sum.
- Calculate total resistance values in series/parallel networks.
Calculations in Series & Parallel Resistor Networks
Components, including resistors in a circuit may be connected together in two ways:
IN SERIES, so that the same current flows through all the components but a different potential difference (voltage) can exist across each one.
IN PARALLEL, so that the same potential difference (voltage) exists across all the components but each component may carry a different current.
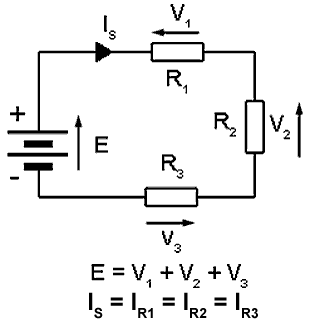
Fig. 4.2.1 Resistors in Series
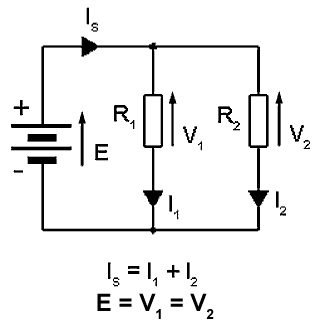
Fig. 4.2.2 Resistors in Parallel
In either case (for resistors) the total resistance of that part of the circuit containing the resistors can be calculated using the methods described below.
Being able to calculate the combined (total) value of resistors in this way makes it easy to work out unknown values of resistance, current and voltage for quite complex circuits using relatively simple methods. This is of great use in fault finding.
BEFORE GOING ANY FURTHER, PRACTICE USING THE FORMULAE FOR CALCULATING THE TOTAL VALUES OF SERIES AND PARALLEL RESISTORS.
For resistors in series:
The total resistance of two or more resistors connected in series is given by simply adding the individual values of the resistors to find the total sum (RTOT):
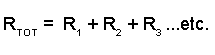
For resistors in parallel:
To calculate the total resistance of a circuit that involves parallel resistors the following formula can be used.
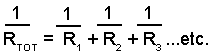
Notice however that this formula does NOT give you the total resistance RTOT. It gives you the RECIPROCAL of RTOT or:
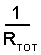
This is a very different value - and is NOT the total resistance. It is 1 divided by RTOT. To obtain the correct value for RTOT (which will be reciprocal of 1/RTOT, i.e. RTOT/1 simply press the reciprocal key on your calculator (marked 1/x or x-1).
Another way to calculate parallel circuits.
The total Resistance of two resistors in parallel that does not involve reciprocals is given by:
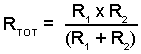
This formula is often referred to as ‘Product over Sum’.
Does it only calculate TWO resistors in parallel? Well, yes, but that´s not a big problem. If there are more than two parallel resistors, just choose two of them and work out the total resistance for these two - then use that total as if it was a single resistor and make another pair with a third resistor. Work out the new total, and so on until you have included all the parallel resistors in that particular network.
Oh, one more thing to remember about product over sum, see the brackets around the sum (bottom part) of the formula? That means you have to work this out BEFORE you use it to divide the product (top part) by. If you don't, your answer will be wrong.
Sounds complicated? Not really, its just a matter of repetition, and in practice you don´t often come across many parallel networks with much more than two resistors. Still, which formula you choose is up to you, reciprocals or product-over-sum.
Tips
Using the Reciprocal Method
If you use the RECIPROCAL METHOD for parallel circuits DON'T FORGET, when you have added the reciprocals of the individual resistors - You must find the reciprocal again.1/R1+1/R2+1/R3 = 1/RTOT and to find RTOT you must find the reciprocal of 1/RTOT.
Simplifying Circuits
For combined series and parallel circuits, work out a section of the circuit (series or parallel) first. Then re-draw the circuit replacing the section you have found the resistance of, with a single resistor. You now have a simplified circuit in which to find RTOT.
You can use the "product over sum" formula:
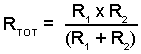
For circuits with more than two parallel resistors, simply work out two parallel resistors at a time using the product over sum formula, and then re-draw the circuit replacing the two resistors with a single resistor whose value is the combined resistance of the two.
Now you can use your first combined value as a single resistor with the next parallel resistor, and so on. In this way a large number of parallel resistors can be worked out using product over sum.
When all the parallel resistors are the same value.
If a number of identical parallel resistors are connected, the total resistance will be the resistor value multiplied by the reciprocal of the number of resistors.
i.e. Two 12K resistors in parallel have a combined resistance of
12K x 1/2 =6K
Three 12K resistors in parallel have a combined resistance of
12K x 1/3 = 4K etc.
Checking your answer
The combined value of any number of parallel resistors will always be LESS than the value of the smallest individual resistor in the network. Use this fact to check your answers.
Series and Parallel Combined
Try a few calculations based on series and parallel resistor networks. For these you just need to use the information on this page and the "Resistor Calculations Tips" page. You are asked to work out the total resistance for each circuit. You can choose which formula to use
You can also find help with the maths by downloading our free Maths Tips booklet.
Before starting, think about these few tips. They will make the problems easier if you follow them carefully.
1. Work out the answers using pencil and paper; redraw the circuit you are working on.
2. Of course the answer is not just a number, it will be a certain number of Ohms, don't forget to show the correct unit (e.g. Ω, KΩ or MΩ) or your answer is meaningless.
3. When you put values into your calculator convert all KΩ or MΩ values to Ohms by using the EXP key. If you slip up here it will give get really stupid answers, thousands of times too big or too small.
So now you have read these instructions, you are ready to start. Here is a way to solve a typical problem on paper so (with practice) you don't get confused.
Series and Parallel Circuit Example.
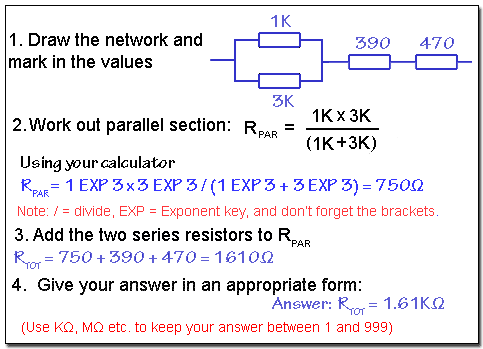
Ok, well plenty to remember there, so why not try some practice questions in Resistors Module 4.5 on finding the total resistance of some resistor networks?
Google Ads


