Module 1.4
Signed Binary
- After studying this section, you should be able to:
- Recognise numbers using Signed Binary Notation.
- • Identify positive binary numbers.
- • Identify negative binary numbers.
- Understand Signed Binary arithmetic
- • Number representation.
- • Advantages of Signed Binary for arithmetic.
- • Disadvantages of Signed Binary for arithmetic.
Signed Binary Notation
All the binary arithmetic problems looked at in Module 1.3 used only POSITIVE numbers. The reason for this is that it is not possible in PURE binary to signify whether a number is positive or negative. This of course would present a problem in any but the simplest of arithmetic.
There are a number of ways in which binary numbers can represent both positive and negative values, 8 bit systems for example normally use one bit of the byte to represent either + or − and the remaining 7 bits to give the value. One of the simplest of these systems is SIGNED BINARY, also often called ‘Sign and Magnitude’, which exists in several similar versions, but is commonly an 8 bit system that uses the most significant bit (msb) to indicate a positive or a negative value. By convention, a 0 in this position indicates that the number given by the remaining 7 bits is positive, and a most significant bit of 1 indicates that the number is negative.
For example:
+4510 in signed binary is (0)01011012
-4510 in signed binary is (1)01011012
Note:
The brackets around the msb (the sign bit) are included here for clarity but brackets are not normally used. Because only 7 bits are used for the actual number, the values the system can represent range from is −12710 or 111111112, to +12710.
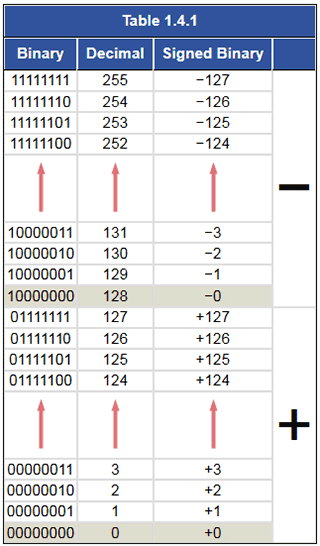
A comparison between signed binary, pure binary and decimal numbers is shown in Table 1.4.1. Notice that in the signed binary representation of positive numbers between +010 and +12710, all the positive values are just the same as in pure binary. However the pure binary values equivalents of +12810 to +25510 are now considered to represent negative values −0 to −127.
This also means that 010 can be represented by 000000002 (which is also 0 in pure binary and in decimal) and by 100000002 (which is equivalent to 128 in pure binary and in decimal).

Fig. 1.4.1 Adding Positive Numbers in Signed Binary
Signed Binary Arithmetic
Because the signed binary system now contains both positive and negative values, calculation performed with signed binary arithmetic should be more flexible. Subtraction now becomes possible by adding a negative number to a positive number, without the problems of borrow and payback described in Number Systems Module 1.3. However there are still problems. Look at the two examples illustrated in Fig. 1.4.1 and 1.4.2, using signed binary notation.

Fig. 1.4.2 Adding Positive & Negative Numbers in Signed Binary
In Fig. 1.4.1 two positive (msb = 0) numbers are added and the correct answer is obtained. This is really no different to adding two numbers in pure binary as described Number Systems Module 1.3.
In Fig. 1.4.2 however, the negative number −5 is added to +7, the same action in fact as SUBTRACTING 5 from 7, which means that subtraction should be possible by merely adding a negative number to a positive number. Although this principle works in the decimal version the result using signed binary is 100011002 or −1210 which of course is wrong, the result of 7 − 5 should be +2.
Although signed binary can represent positive and negative numbers, if it is used for calculations, some special action would need to be taken, depending on the sign of the numbers used, and how the two values for 0 are handled, to obtain the correct result. Whilst signed binary does solve the problem of REPRESENTING positive and negative numbers in binary, and to some extent carrying out binary arithmetic, there are better sign and magnitude systems for performing binary arithmetic. These systems are the ONES COMPLEMENT and TWOS COMPLEMENT systems, which are described in Number Systems Module 1.5.


